YANN (Yet Another Neural Network) Backpropogation Example

1. Introduction

This document demonstrates the mechanics, underlying a simple but not completely simplistic fully connected neural network (NN). In particular the multivariable mathematics involved in backpropogation is illustrated with a running example, which eschews the irritating handwavy approach found in many books, all of which seem to assume you can't differentiate (some of these texts do cover differentiation but they assume the single variable case, while even simple NNs are multivariate in real life). The example will utilise matrix multiplication of Jacobians for implementing the chain rule.

In order to validate our results along the way a (low level tensor based) Pytorch implementation is used to output gradients and final weights and these values are utilised to check the mathematics. After completing the mathematical description, the example network is also implemented in the higher level API available in PyTorch, along with a low and high level implementation in Tensorflow 2, with the low level implementation utilising the GradientTape API while the higher level version is implemented using the new tf.keras API.

We start with an image illustrating the example network:

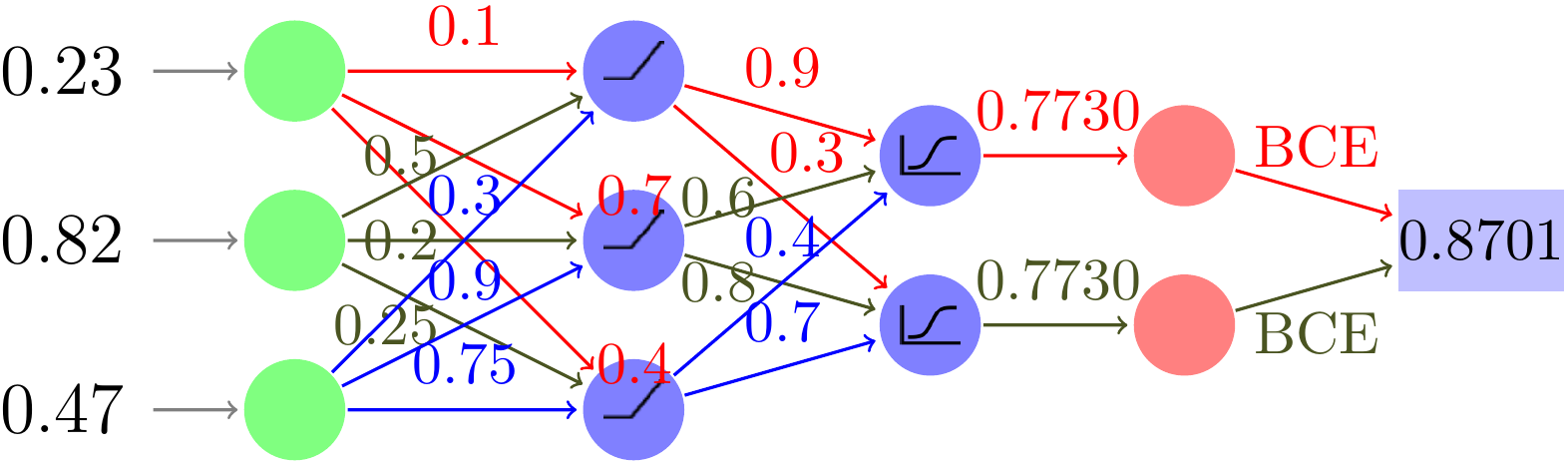
It comprises 3 inputs, two hidden layers of size 3 and 2 respectively with two outputs evaluated by a Binary CrossEntropy loss function. The first hidden layer has a RELU activation function while the second uses a Sigmoid to provide probabilities.

The document is implemented the open source SageMath Computer Algebra System (CAS), and the notebook is also available.

2. PyTorch Tensor Version

import torch
import torch.nn.functional as fn
import torch.optim as opt

INPUT = torch.FloatTensor( [ 0.23, 0.82, 0.47 ]  )
LABEL = target = torch.FloatTensor([1, 0])

def run():
   w1 = torch.tensor([ [0.1, 0.5, 0.3 ], [0.7, 0.2, 0.9 ], [0.4, 0.25, 0.75] ], requires_grad=True)
   b1 = torch.tensor( [0.0, 0.0, 0.0], requires_grad=True)
   w2 = torch.tensor([ [0.9, 0.6, 0.4 ], [0.3, 0.8, 0.7] ], requires_grad=True)
   b2 = torch.tensor( [0.0, 0.0], requires_grad=True)
   a1 = torch.relu(w1 @ INPUT + b1)
   optimiser = opt.SGD((w1, b1, w2, b2), lr=0.01)
   optimiser.zero_grad()
   print('activated 1 = ', a1, "Bias 2 = ", b2)
   a2 = torch.sigmoid(w2 @ a1 + b2)
   print('activated 2 = ', a2)
   loss = fn.binary_cross_entropy(a2, LABEL, weight=None, reduction='mean')
   print('Loss =', loss)
   # loss.backward()
   loss.backward()
   print('grad W2 = \n', w2.grad)
   print('grad b2 = ', b2.grad)
   print('grad W1 = \n', w1.grad)
   print('grad b1 = ', b1.grad)
   optimiser.step()
   print("Layer 1 Weights\n", w1.data)
   print("Layer 1 Bias", b1.data)
   print('======================')
   print("Layer 2 Weights\n", w2.data)
   print("Layer 2 Bias", b2.data)

def main(argv):
   run()

producing:

activated 1 =  tensor([0.5740, 0.7480, 0.6495], grad_fn=<ReluBackward0>) Bias 2 =  tensor([0., 0.], requires_grad=True)
activated 2 =  tensor([0.7730, 0.7730], grad_fn=<SigmoidBackward>)
Loss = tensor(0.8701, grad_fn=<BinaryCrossEntropyBackward>)
grad W2 = 
 tensor([[-0.0652, -0.0849, -0.0737],
        [ 0.2218,  0.2891,  0.2510]])
grad b2 =  tensor([-0.1135,  0.3865])
grad W1 = 
 tensor([[0.0032, 0.0113, 0.0065],
        [0.0555, 0.1977, 0.1133],
        [0.0518, 0.1846, 0.1058]])
grad b1 =  tensor([0.0138, 0.2411, 0.2251])
Layer 1 Weights
 tensor([[0.1000, 0.4999, 0.2999],
        [0.6994, 0.1980, 0.8989],
        [0.3995, 0.2482, 0.7489]])
Layer 1 Bias tensor([-0.0001, -0.0024, -0.0023])
======================
Layer 2 Weights
 tensor([[0.9007, 0.6008, 0.4007],
        [0.2978, 0.7971, 0.6975]])
Layer 2 Bias tensor([ 0.0011, -0.0039])

3. Mathematics

3.1 Forward Pass

We start by doing the forward pass and recording the numeric results for later use during backpropogation.

%display latex
viewer3D = 'threejs'
clear_vars()
#sigmoid(x) = 1 / (1 + exp(-x))
def sigmoid(v): # MATLAB Symbolic AKA Maple is a little better here as functions work transparently with vectors and scalars
    vv = [None] * len(v)
    for i in range(0, len(v)):
        vv[i] = 1 / (1 + exp(-v[i]))  
    return vv        
# ident(x) = x
# relu = piecewise([[(-infinity, 0), 0], [(0, infinity), ident]])
def relu(v):
    vv = [None] * len(v)
    for i in range(0, len(v)):
        vv[i] = max(0,v[i])
    return vector(SR, vv)        
bce(l, y) = l*log(y) + (1 - l)*log(1 - y)

def relun(x):
    try:
        return max(0,x)
    except:
        xx = [None] * len(x)
        for i in range(0, len(x)):
            xx[i] = max(0, x[i])
        return xx    
def sigmoidn(x):
    try:
        return 1 / (1 + exp(-x))
    except:
        xx = [None] * len(x)
        for i in range(0, len(x)):
            xx[i] = 1 / (1 + exp(-x[i]))  
        return xx    
def bcen(l, y):
    return l*log(y) + (1 - l)*log(1 - y)
            
        
Xn = vector([0.23, 0.82, 0.47 ])
W1n = Matrix([ [0.1, 0.5, 0.3], [0.7, 0.2, 0.9], [0.4, 0.25, 0.75] ])
W2n = Matrix([ [ 0.9, 0.6, 0.4],  [0.3, 0.8, 0.7] ])
B1n = vector([0.0, 0.0, 0.0])
B2n = vector([0.0, 0.0])
l1n = 1.0
l2n = 0.0

Z1n = W1n * Xn + B1n;
# Z1n.n(digits=5)
A1n = relun(Z1n);
print('activated 1 = ', A1n)
Z2n = W2n * A1n + B2n
A2n = sigmoidn(Z2n)
print('activated 2 = ', A2n)
# vpa([bce(l1n,A2n(1)), bce(l2n,A2n(2))], 5)
En = -(bcen(l1n,A2n[0]) + bcen(l2n,A2n[1]))/2
print('Loss = ', En)

activated 1 =  (0.574000000000000, 0.748000000000000, 0.649500000000000)
activated 2 =  [0.772977357985251, 0.772986132033595]
Loss =  0.870124846460152

As can be seen by comparing the feed forward results to the PyTorch ones everything matches.

3.2 Backpropogation

3.2.1 Hidden Layer 2 Weight Gradient

Next we start backpropogation by calculating the gradients for the second set of weights and biases. The error $E$ is expressed in terms of the output from the 2nd activation layer seen as probabilities $a_{2,i}$ and the labels for each output $l_i$:

$E = -\frac{1}{N} \sum_{i=1}^{N} l_{i} \cdot \log \left(a_{2,i})\right)+\left(1-l_i\right) \cdot \log \left(1-a_{2,i})\right)$

In this case $N = 2$ so $i \in 1,2$ so the equation in this case is:

$-\frac{1}{2}(l_1\log(a_{2,1}) + (1 - l_1)\log(1 - a_{2,1}) + l_2\log(a_{2,2}) + (1 - l_2)\log(1 - a_{2,2})$.

The 2nd activation layer is found in terms of the previous linear output $\vec{z_2} = (z_{2,1}, z_{2,2})$ using the Sigmoid:

$\sigma_2(\vec{z_2}) = (\frac{1} {1 + e^{-z_{2,1}}}, \frac{1} {1 + e^{-z_{2,2}}})$

The linear output $z_2$ used as input to the sigmoid above is found in terms of the the output of the first activation layer $a_1 = (a_{1,1}, a_{1,2}, a_{1,3})$, the second weight matrix $W_2$ and the 2nd bias vector $\vec{b_2}$:

$\mathcal{L}_2(\vec{a_1}) = \vec{z_2} = W_2 \vec{a_1}^\intercal + \vec{b_2}$

$E$ above is the result of function composition ie $(E \circ \sigma \circ \mathcal{L}_2)(\vec{a_1})$ We want the gradients w.r.t the weights in $W_2$ and the biases in $\vec{b_2}$ $\therefore$ we may use the (multivariable) chain rule: $D(E \circ \sigma \circ \mathcal{L}_2)(\vec{a_1}) = D(E)[ \sigma_2 \circ \mathcal{L}_2(\sigma_1)] \cdot D( \sigma_2 \circ \mathcal{L}_2)[\sigma_1] = J_{a_2}(E)[ \sigma_2 \circ \mathcal{L}_2(\sigma_1)] \cdot J_{z_2}(\sigma_2)[\mathcal{L}_2(\sigma_1)] \cdot J_{W_2}(\mathcal{L}_2)[\vec{a_1}]$

where $\vec{a1}$ is the output from activation layer 1 (relu).

The square bracket notation $[expr]$ means "evaluated at expr", and we know what these values are from the forward pass. Also as we are doing multivariable differentation, the D's above can be seen as Jacobians (the $J$'s in the final part of the expression). In order to make it simpler to distinguish between weights and biases we will use separate expressions for the final term one with a Jacobian in terms of the weights and the other in terms of the bias, although computationally this is unnecessary as the output from a single can be reshaped appropriately. The Sagemath representation of the above follows:

var('a_11 a_12 a_13 a_21 a_22 l_1 l_2 z_21 z_22', domain='real')
var('w2_11 w2_12 w2_21 w2_22 w2_31 w2_32 b2_1 b2_2', domain='real')
W2 = matrix(SR, 3, 2, [w2_11, w2_12,  w2_21, w2_22,  w2_31, w2_32])
W2 = W2.transpose()
B2 = vector(SR, (b2_1, b2_2))
a_1 = vector(SR, (a_11, a_12, a_13))
E = -(bce(l_1, a_21) + bce(l_2, a_22))/2
JE = jacobian(E, (a_21, a_22)).substitute(a_21=A2n[0], a_22=A2n[1], l_1=l1n, l_2=l2n)
z_2 = vector(SR, (z_21, z_22))
a_2 = sigmoid(z_2)
JSig = jacobian(a_2, (z_21, z_22)).substitute(z_21=Z2n[0], z_22=Z2n[1])
Ll2 = W2*a_1 + B2
Jlw2 = jacobian(Ll2, W2.list()).substitute(a_11=A1n[0], a_12=A1n[1], a_13=A1n[2])
Jlb2 = jacobian(Ll2, B2.list())
Dw2 = JE*JSig*Jlw2
Dw2o = matrix(RR, [ Dw2[0][0:3], Dw2[0][3:]])
Db2 = JE*JSig*Jlb2
print('---------- Weights 2 Grad ---------------')
# pretty_print(JE.n(digits=5),JSig.n(digits=5),Jlw2.n(digits=5),'=')
# pretty_print(Dw2.n(digits=5))
pretty_print(Dw2o.n(digits=5))
print('----------Bias 2 Grad ---------------')
# pretty_print(JE.n(digits=5),JSig.n(digits=5),Jlb2.n(digits=5),'=')
pretty_print(Db2.n(digits=5))

---------- Weights 2 Grad ---------------

$$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\begin{array}{rrr} -0.065156 & -0.084906 & -0.073726 \\ 0.22185 & 0.28910 & 0.25103 \end{array}\right)$$

----------Bias 2 Grad ---------------

$$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\begin{array}{rr} -0.11351 & 0.38649 \end{array}\right)$$

The weight matrix gradient reported above corresponds to the gradient matrix for W2 reported by Pytorch in the PyTorch section above:

grad W2 = tensor([[-0.0652, -0.0849, -0.0737], [ 0.2218, 0.2891, 0.2510]])

as does the bias gradient

grad b2 = tensor([-0.1135, 0.3865])

3.2.2 Layer 1 Weight Gradient

The next step is to find the gradients w.r.t the first layer weights and biases. First, the activation layer 1 whose output was used in $\mathcal{L}_2$ above can be expressed in terms of $\vec{z_1} = (z_{1,1}, z_{1,2}, z_{1,3})$, the output of the first linear layer $\mathcal{L}_1$:

$\vec{\hat a_1} = (a_{1,1}, a_{1,2}, a_{1,3}) = relu_1(\vec{z_1}) = relu(z_{1,1}, z_{1,2}, z_{1,3})$

and $\vec{z_1}$ is the output of the first linear layer $\mathcal{L}_1(\vec{x}) = W_1 \vec{x} + \vec{b_1}$ where $\vec{x} = (x_1, x_2, x_3)$ is the original input.

The function composition for the above is is $(relu \circ \mathcal{L}_1)(\vec{x})$. Before applying the chain rule again however we need first note that the Jacobean in the chain rule composition in Section 3.2.1 above was in terms of the layer 2 weights so as to obtain the weights, but in order to continue backpropogation the $J_{W_2}(\mathcal{L}_2)[\vec{\hat a_1}]$ term in the chain rule expression $J(E)[ \sigma_2 \circ \mathcal{L}_2(\sigma_1)] \cdot J(\sigma_2)[\mathcal{L}_2(\sigma_1)] \cdot J_{W_2}(\mathcal{L}_2)[\vec{\hat a_1}]$ needs to change to $J_{a_1}(\mathcal{L}_2)[\vec{\hat a_1}]$, that is to differentiate w.r.t the first layer activation output. This enables the chain differentiation to continue with the correct shapes for the matrices.

Ll2 = W2*a_1 + B2
Jla2 = jacobian(Ll2, (a_11, a_12, a_13)).substitute(w2_11=W2n[0][0], w2_21=W2n[0][1], w2_31=W2n[0][2], w2_12=W2n[1][0], w2_22=W2n[1][1], w2_32=W2n[1][2])

The chain rule evaluation can then be performed on the expression below:

$D(E \circ \sigma \circ \mathcal{L}_2 \circ relu \circ \mathcal{L}_1)(\vec{x}) = J(E)[ \sigma_2 \circ \mathcal{L}_2(\sigma_1)] \cdot J(\sigma_2)[\mathcal{L}_2(\sigma_1)] \cdot J_{\vec{a_1}}(\mathcal{L}_2)[\vec{\hat a_1}] \cdot J(relu)[\mathcal{L}_1(\vec{x})] \cdot J(\mathcal{L}_1)[\vec{x}]$

(Note we assume the input domain to be positive for this example (which it is for the numeric values) in order to not have branched outputs for the relu)

var('x_1 x_2 x_3 z1_1 z1_2  z1_3', domain='positive')
x = vector(SR, (x_1, x_2, x_3))
var('w_11 w_12 w_13 w_21 w_22 w_23 w_31 w_32 w_33 b1_1 b1_2 b1_3', domain='real')
W1 = matrix(SR, [ [w_11, w_12, w_13],  [w_21, w_22, w_23], [w_31, w_32, w_33] ])
B1 = vector(SR, (b1_1, b1_2, b1_3))
W1 = W1.transpose()
Ll1 = W1*x + B1
Jlw1 = jacobian(Ll1, W1.list()).substitute(x_1=Xn[0], x_2=Xn[1], x_3=Xn[2])
Jlb1 = jacobian(Ll1, B1.list()).substitute(x_1=Xn[0], x_2=Xn[1], x_3=Xn[2])
z_1 = vector(SR, (z1_1, z1_2, z1_3))
A1 = relu(z_1)
Ja1z = jacobian(A1, [z1_1, z1_2, z1_3])

DW1 = JE*JSig*Jla2*Ja1z*Jlw1
DW1o = matrix(RR, [ DW1[0][0:3], DW1[0][3:6], DW1[0][6:] ])
DB1 = JE*JSig*Jla2*Ja1z*Jlb1
print('---------- Weights 1 Grad ---------------')
pretty_print(DW1o.n(digits=5))
print('---------- Bias 1 Grad ---------------')
pretty_print(DB1.n(digits=5))

---------- Weights 1 Grad ---------------

$$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\begin{array}{rrr} 0.0031712 & 0.011306 & 0.0064802 \\ 0.055450 & 0.19769 & 0.11331 \\ 0.051782 & 0.18462 & 0.10582 \end{array}\right)$$

---------- Bias 1 Grad ---------------

$$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\begin{array}{rrr} 0.013788 & 0.24109 & 0.22514 \end{array}\right)$$

The weight matrix gradient reported above corresponds to the gradient matrix for W2 reported by Pytorch in the PyTorch section above:

grad W1 = tensor([[0.0032, 0.0113, 0.0065], [0.0555, 0.1977, 0.1133], [0.0518, 0.1846, 0.1058]])

grad b1 = tensor([0.0138, 0.2411, 0.2251])

Note the approach here is not the way a real backpropogation algorithm would work, as its just a brute force application of the chain rule. See [Margossian, Charles, 2018] for a description of the real back (and forward) propogation algorithms.

Assuming a learning rate of 0.01 the weights can then be adjusted:

print('Weights 1')
pretty_print(-0.01*DW1o + W1n)
print('Weights 2')
pretty_print(-0.01*Dw2o + W2n)

Weights 1

$$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\begin{array}{rrr} 0.0999682882189337 & 0.499886940606633 & 0.299935197664777 \\ 0.699445498381519 & 0.198023081186286 & 0.898866887997018 \\ 0.399482176579040 & 0.248153846933968 & 0.748941839096299 \end{array}\right)$$

Weights 2

$$\newcommand{\Bold}[1]{\mathbf{#1}}\left(\begin{array}{rrr} 0.900651554982582 & 0.600849064681135 & 0.400737256029943 \\ 0.297781529801064 & 0.797109031866194 & 0.697489727536221 \end{array}\right)$$

which corresponds to the PyTorch calculated weights:

Layer 1 Weights

tensor([[0.1000, 0.4999, 0.2999],

    [0.6994, 0.1980, 0.8989],

    [0.3995, 0.2482, 0.7489]])

Layer 1 Bias tensor([-0.0001, -0.0024, -0.0023])

======================

Layer 2 Weights

tensor([[0.9007, 0.6008, 0.4007],

    [0.2978, 0.7971, 0.6975]])

Layer 2 Bias tensor([ 0.0011, -0.0039])

4. PyTorch Model Based Version

import torch
from torch import nn
import torch.optim as opt

WEIGHTS1 = torch.FloatTensor([ [0.1, 0.5, 0.3 ], [0.7, 0.2, 0.9 ], [0.4, 0.25, 0.75] ])
WEIGHTS2 = torch.FloatTensor([ [0.9, 0.6, 0.4 ], [0.3, 0.8, 0.7] ])
TRAIN = torch.FloatTensor( [ 0.23, 0.82, 0.47 ]  )
LABEL = target = torch.FloatTensor([1, 0])

class SimplisticNN(nn.Module):
   def __init__(self):
      super(SimplisticNN, self).__init__()
      self.hidden1 = nn.Linear(3, 2, bias=True)
      self.hidden1.weight.data = WEIGHTS1
      self.hidden1.bias.data = torch.FloatTensor( [0, 0, 0])
      self.activation1 = torch.nn.ReLU()

      self.hidden2 = nn.Linear(3, 2, bias=True)
      self.hidden2.weight.data = WEIGHTS2
      self.hidden2.bias.data = torch.FloatTensor([0, 0])
      self.activation2 = nn.Sigmoid()
      self.loss = nn.BCELoss(reduction='mean')

   def forward(self, batch):
      hidden1 = self.hidden1(batch)
      activated1 = self.activation1(hidden1)
      hidden2 = self.hidden2(activated1)
      out = self.activation2(hidden2)
      return out

model = SimplisticNN()
# model.train()
y = model(TRAIN)
output = model.loss(y, LABEL)
# for param in model.parameters():
#    print(str(param))
optimiser = opt.SGD(model.parameters(), lr=0.01)
optimiser.zero_grad()
output.backward()
print('grad W2 = \n', model.hidden2.weight.grad)
print('grad b2 = ', model.hidden2.bias.grad)
print('grad W1 = \n',model.hidden1.weight.grad)
print('grad b1 = ', model.hidden1.bias.grad)
optimiser.step()

print('Loss =', output)
print("Layer 1 Weights\n", model.hidden1.weight.data)
print("Layer 1 Bias\n", model.hidden1.bias.data)
print('======================')
print("Layer 2 Weights\n", model.hidden2.weight.data)
print("Layer 2 Bias\n", model.hidden2.bias.data)

producing:

grad W2 = 
 tensor([[-0.0652, -0.0849, -0.0737],
        [ 0.2218,  0.2891,  0.2510]])
grad b2 =  tensor([-0.1135,  0.3865])
grad W1 = 
 tensor([[0.0032, 0.0113, 0.0065],
        [0.0555, 0.1977, 0.1133],
        [0.0518, 0.1846, 0.1058]])
grad b1 =  tensor([0.0138, 0.2411, 0.2251])
Loss = tensor(0.8701, grad_fn=<BinaryCrossEntropyBackward>)
Layer 1 Weights
 tensor([[0.1000, 0.4999, 0.2999],
        [0.6994, 0.1980, 0.8989],
        [0.3995, 0.2482, 0.7489]])
Layer 1 Bias
 tensor([-0.0001, -0.0024, -0.0023])
======================
Layer 2 Weights
 tensor([[0.9007, 0.6008, 0.4007],
        [0.2978, 0.7971, 0.6975]])
Layer 2 Bias
 tensor([ 0.0011, -0.0039])

5. TensorFlow 2 Versions

5.1 Using GradientTape

import numpy as np
import tensorflow as tf
import tensorflow.keras.losses as kl

TRAIN = np.array( [ [0.23, 0.82, 0.47 ] ]  )
LABEL = np.array([1.0, 0.0 ] )
WEIGHTS1 = np.array([ [0.1, 0.5, 0.3 ], [0.7, 0.2, 0.9 ], [0.4, 0.25, 0.75]  ])
WEIGHTS2 = np.array([ [0.9, 0.6, 0.4 ], [0.3, 0.8, 0.7] ])

def run():
   input = tf.transpose(tf.convert_to_tensor(TRAIN, dtype=tf.float32))
   labels = tf.transpose(tf.convert_to_tensor(LABEL, dtype=tf.float32))
   w1 = tf.Variable(tf.convert_to_tensor(WEIGHTS1, dtype=tf.float32))
   w2 = tf.Variable(tf.convert_to_tensor(WEIGHTS2, dtype=tf.float32))
   b1 = tf.Variable(tf.transpose(tf.convert_to_tensor([ [0.0, 0.0, 0.0] ], dtype=tf.float32)))
   b2 = tf.Variable(tf.transpose(tf.convert_to_tensor( [ [0.0, 0.0] ], dtype=tf.float32)))
   dependents = (w1, b1, w2, b2)
   optimizer = tf.optimizers.SGD(0.01)
   with tf.GradientTape(persistent=True) as dag:
      dag.watch(w1)
      dag.watch(w2)
      dag.watch(b1)
      dag.watch(b2)
      z1 = tf.linalg.matmul(w1, input)
      a1 = tf.keras.activations.relu(tf.math.add(z1, b1))
      # dag.watch(a1)
      z2 = tf.linalg.matmul(w2, a1)
      a2 = tf.keras.activations.sigmoid(tf.math.add(z2, b2))
      # dag.watch(a2)
      # print(a2)
      loss = tf.reduce_mean(kl.binary_crossentropy(labels, a2))
      print("Loss =", loss)
   grad = dag.gradient(loss, dependents)
   # print(str(grad))
   optimizer.apply_gradients(zip(grad, dependents))
   # print(dag.gradient(loss, dependents))
   print(dag.gradient(loss, w1))
   print(dag.gradient(loss, b1))
   print('grad W2 = \n', dag.gradient(loss, w2))
   print('grad b2 = ', dag.gradient(loss, b2))
   print('grad W1 = \n', dag.gradient(loss, w2))
   print('grad b1 = ', dag.gradient(loss, b1))
   print("Layer 1 Weights\n", w1)
   print("Layer 1 Bias",  b1)
   print("Layer 2 Weights\n", w2)
   print("Layer 2 Bias",  b2)

tf.config.set_visible_devices([], 'GPU') # Disable GPU
run()

producing:

Loss = tf.Tensor(0.870112, shape=(), dtype=float32)
tf.Tensor(
[[0.03767115 0.13430585 0.07698018]
 [0.04395014 0.15669179 0.08981115]
 [0.03453232 0.12311524 0.07056605]], shape=(3, 3), dtype=float32)
tf.Tensor(
[[0.16378762]
 [0.19108756]
 [0.15014054]], shape=(3, 1), dtype=float32)
grad W2 = 
 tf.Tensor(
[[0.07834444 0.10209345 0.08864933]
 [0.07834699 0.10209677 0.08865222]], shape=(2, 3), dtype=float32)
grad b2 =  tf.Tensor(
[[0.13648857]
 [0.13649301]], shape=(2, 1), dtype=float32)
grad W1 = 
 tf.Tensor(
[[0.07834444 0.10209345 0.08864933]
 [0.07834699 0.10209677 0.08865222]], shape=(2, 3), dtype=float32)
grad b1 =  tf.Tensor(
[[0.16378762]
 [0.19108756]
 [0.15014054]], shape=(3, 1), dtype=float32)
Layer 1 Weights
 <tf.Variable 'Variable:0' shape=(3, 3) dtype=float32, numpy=
array([[0.09962329, 0.49865693, 0.29923022],
       [0.69956046, 0.19843309, 0.89910185],
       [0.3996547 , 0.24876885, 0.74929434]], dtype=float32)>
Layer 1 Bias <tf.Variable 'Variable:0' shape=(3, 1) dtype=float32, numpy=
array([[-0.00163788],
       [-0.00191088],
       [-0.00150141]], dtype=float32)>
Layer 2 Weights
 <tf.Variable 'Variable:0' shape=(2, 3) dtype=float32, numpy=
array([[0.89921653, 0.5989791 , 0.3991135 ],
       [0.29921654, 0.79897904, 0.6991135 ]], dtype=float32)>
Layer 2 Bias <tf.Variable 'Variable:0' shape=(2, 1) dtype=float32, numpy=
array([[-0.00136489],
       [-0.00136493]], dtype=float32)>

5.2 Using tf.keras

Displaying the gradients is left as an exercise for the reader (i.e. I couldn't find any simple way of doing it).

import numpy as np
import tensorflow as tf
from tensorflow import keras

TRAIN = np.array( [ [ 0.23, 0.82, 0.47 ] ])
LABEL = np.array( [ [ 1.0, 0.0 ] ])
WEIGHTS1 = np.array([ [0.1, 0.5, 0.3 ], [0.7, 0.2, 0.9 ], [0.4, 0.25, 0.75] ])
WEIGHTS2 = np.array([ [0.9, 0.6, 0.4 ], [0.3, 0.8, 0.7] ])

def setup():
   weights1 = tf.constant_initializer(WEIGHTS1)
   weights2 = tf.constant_initializer(WEIGHTS2)
   m = tf.keras.models.Sequential()
   m.add(keras.layers.Dense(3, input_shape=(3,), kernel_initializer=weights1, use_bias=True, bias_initializer='zeros', activation='relu'))
   m.add(keras.layers.Dense(2, kernel_initializer=weights2, use_bias=True, bias_initializer='zeros', activation='sigmoid'))
   m.compile(loss='binary_crossentropy', optimizer='SGD')
#   from tensorflow.keras.utils import plot_model
#   plot_model(m, to_file='model.png', show_shapes=True, expand_nested=True)
   return m

tf.config.set_visible_devices([], 'GPU') # 2.1
#my_devices = tf.config.experimental.list_physical_devices(device_type='CPU') #2.0
#tf.config.experimental.set_visible_devices(devices= my_devices, device_type='CPU') #2.0
model = setup()

_ = model.fit(TRAIN, LABEL, batch_size=1, epochs=1, verbose=False)
print(model.weights[0])
print('----------------------------------------')
print(model.weights[1])
print('=========================================')
print(model.weights[2])
print('----------------------------------------')
print(model.weights[3])

producing:

{'batch': 0, 'size': 1, 'loss': 0.8878588}
<tf.Variable 'dense/kernel:0' shape=(3, 3) dtype=float32, numpy=
array([[0.09959406, 0.49978882, 0.2994854 ],
       [0.6985527 , 0.1992471 , 0.89816517],
       [0.39917046, 0.24956846, 0.74894834]], dtype=float32)>
----------------------------------------
<tf.Variable 'dense/bias:0' shape=(3,) dtype=float32, numpy=array([-0.00176497, -0.00091817, -0.00223756], dtype=float32)>
=========================================
<tf.Variable 'dense_1/kernel:0' shape=(3, 2) dtype=float32, numpy=
array([[0.90056026, 0.59685045],
       [0.40028298, 0.2984092 ],
       [0.80082756, 0.69534785]], dtype=float32)>
----------------------------------------
<tf.Variable 'dense_1/bias:0' shape=(2,) dtype=float32, numpy=array([ 0.00071371, -0.00401219], dtype=float32)>